Оглавление
ВведениеГномон. Полуденная линия
Гномон. Координаты
Уравнение времени
Размер Земли
Размер Луны
Лунный "альпинизм"
Лампочка и Солнце
Прав ли художник?
История почтовой марки
Легенда о Медведице
Звездные часы
Ориентирование на местности
Звезды за занавеской
Транзит Венеры
Челябинский метеорит
Лунный "альпинизм"
При наблюдениях Луны даже в скромные любительские телескопы открываются потрясающие картины - кратеры всевозможных размеров, бескрайние моря застывшей лавы, трещины и горные пики... Конечно, Луна была одним из первых объектов, на которые направил свой телескоп Галилео Галилей - именно он первым описал рельеф нашего спутника, он же предложил и первые методы его исследования. Попробуем и мы заняться своеобразным "альпинизмом" и исследовать горы Луны (кстати, горные цепи названы вполне привычно, по-земному - там тоже есть Карпаты, Кавказ, Алтай, Альпы... так что "альпинизм" - слово вполне подходящее и для Луны)
Первый метод определения высоты лунных гор предложил Галилей - по угловому расстоянию от терминатора (линии тени), на котором эта вершина скрывается в тени или появляется из тени. Однако мы воспользуемся другим, более универсальным способом, основанном на измерении длины тени, отбрасываемой вершиной.
Для измерений воспользуемся любительской фотографией Луны вблизи третьей четверти. (По этой ссылке можно скачать полноразмерный снимок - именно с ним мы и будем работать, все измерения выполнялись с помощью инструмента "линейка" в программе Adobe Photoshop)
Желательно для удобства измерений сориентировать снимок так, чтобы "рога" лунного диска распологались вертикально. Условно назовем точки пересечения терминатора с диском полюсами, соединяющую их линию центральным меридианом, а серединный перпендикуляр к нему - экватором. Строго говоря, эти определения неправильны, так как они привязаны не к лунным (селенографическим) координатам, а к параметрам освещенности Лунного шара Солнцем, но для наших расчетов именно это и требуется.

На снимке точка O - центр диска Луны, М - гора, высоту которой требуется измерить (в нашем примере это Пико в северной части Моря Дождей). Для этой точки построена параллель (горизонтальная прямая RmMOm). Зелёной кривой отмечено положение терминатора - границы освещенного и темного полушарий Луны и точка пересечения его с паралелью T. (Кстати, чуть южнее этой точки на фото видна ярко освещенная гора Монблан - одна из самых заметных вершин лунных Альп)
Исходная формула очень проста:
Высота горы H=S*tg(α) , где
S - длина тени
α - угол падения солнечных лучей

Необходимо только определить значения входящих в формулу величин. Угол падения лучей α есть разница долгот объекта и терминатора. Его можно определить по проекциям углов LM и LT (на фото проекции обозначены соответственно L'M и L'T). Лучше измерять именно эти углы - от края диска Луны, а не от центрального меридиана, так как его положение может быть определено не совсем точно. Еще одно важное замечание - приведенная выше формула не учитывает кривизну поверхности Луны, а она весьма существенно сказывается на результате, поэтому для уменьшения ошибок разницу долгот объекта и терминатора (или L'M для ее расчета) следует определять по середине тени. Еще один возможный источник ошибок - определение положения терминатора, особенно, как в нашем случае, когда он проходит по гористой местности - в этом случае нужно построить линию терминатора по точкам севернее и южнее, где он проходит по равнинным участкам. Если это невозможно, то придется определять его положение на момент съемки по электронным атласам Луны (например, Virtual Moon Atlas)
Угол падения солнечных лучей
α=LT-LM=arccos((Rφ-LT')/Rφ)-arccos((Rφ-LM')/Rφ) , где
Rφ - радиус параллели на широте объекта φ;
(а для малых углов вблизи центрального меридиана можно считать α=arcsin(α'/Rφ) , где α' - расстояние в пикселах от середины тени до терминатора)
Rφ=Ro*cos(φ); Ro=|NS|/2 - радиус Луны;
φ=arcsin(φ'/Ro)
Угол φ можно также определить графически - он равен величине угла RoORm
Теперь можно перейти к собственно измерению длины тени.

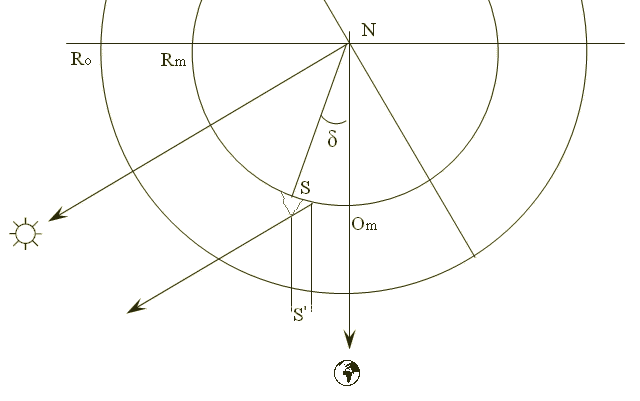
Длина тени
S=k*S'/cos(δ)
δ=arcsin(δ'/Rφ)=arcsin((Rφ-LM')/Rφ) -угол наклона линии тени
k=DЛуны/D=3476/|NS| -масштаб снимка (км/pix)
В нашем случае объект очень близок к центральному меридиану и мы могли бы пренебречь изменением видимой длины тени из-за кривизны лунной поверхности, но в общем случае это необходимо учитывать.
Итак, все готово для проведения расчетов:
Ro=1132 pix; D=2264 pix; k=3780/2264=1.535;
LT'=800 pix;
LM'=700 pix;
φ'=829 pix;
φ=arcsin(φ'/Ro)=47.1°;
Rφ=Ro*cos(φ)=1131*cos(47.1°)=769.4 pix;
α=arccos((Rφ-LT')/Rφ)-arccos((Rφ-LM')/Rφ)=
=arccos(-30.6/769.4)-arccos(69.4/769.4)=7.46°;
S'=14 pix;
δ'=74 pix; δ=arcsin(δ'/Rφ)=arcsin(74'/769.4)=5.5°
S=1.535*14/cos(5.5°)=21.59 км;
H=S*tg(α)=21.59*tg(7.46°)=2.82 км
Приведенная в атласе лунной поверхности высота этой точки относительно восточного подножья горы составляет 2420м, однако расхождение цифр еще не говорит о нашей ошибке - дело в том, что фактически мы измеряем высоту вершины относительно той точки на поверхности Луны, где расположен край тени, отбрасываемой этой вершиной. А поверхность Моря Дождей нельзя считать абсолютно горизонтальной - как раз в этом районе расположены несколько невысоких, но протяженных валов, вполне способных повлиять на результат измерений.