Размер Луны

После установления размеров Земли следующим вполне логичным вопросом стало определение размеров Луны и расстояния до нее. Впервые эту задачу решил, по-видимому, Аристарх в III веке до нашей эры.

Лунные и солнечные затмения всегда привлекали внимание людей - еще бы! - такие события трудно не заметить! Но кроме необычности и красоты этих явлений, они несли и важнейшую информацию об устройстве нашего мира. Попробуем, повторив рассуждения Аристарха, определить по тени взаимные размеры Земли и Луны.

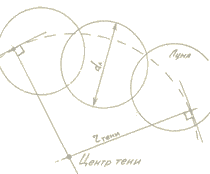
Посмотрите на фотографию - это монтаж трех снимков частного лунного затмения 16-17 августа 2008 года.

На этом снимке очень наглядно видна форма земной тени и можно достаточно точно определить ее размер на расстоянии Луны. Конечно, для определения размеров тени вовсе не обязательно фотографировать ее - достаточно лишь определить продолжительность полной фазы затмения, а это легко можно сделать визуально даже без применения каких-то оптических приборов. (Увы, Аристарх не мог воспользоваться таким способом - точных часов тогда не было ...) В самом деле, период обращения Луны относительно Солнца (синодический месяц) хорошо известен (кстати, наиболее точно он определяется также по наблюдениям затмений) и составляет 29,53 суток. Средняя скорость движения Луны относительно Солнца (и земной тени) составит 0,508°/час, или примерно видимый диаметр Луны в час. Зная продолжительность полной фазы лунного затмения мы можем определить размер земной тени. Правда, чтобы избежать громоздких расчетов, измерения нужно проводить в такое затмение, когда центр Луны максимально близко проходит у центра земной тени. Таким будет, например, затмение 15 июня 2011 года.

Определив одним из этих способов размер тени Земли (выраженный в диаметрах лунного диска) нам осталось только учесть, что тень имеет форму конуса и ее сечение уменьшается с расстоянием. Сечение же конуса полутени увеличивается и на расстоянии Луны область полутени имеет ширину, примерно равную диаметру лунного диска (см. рисунок), это объясняется тем, что видимые угловые размеры Луны и Солнца равны (это особенно хорошо заметно при наблюдениях солнечных затмений).

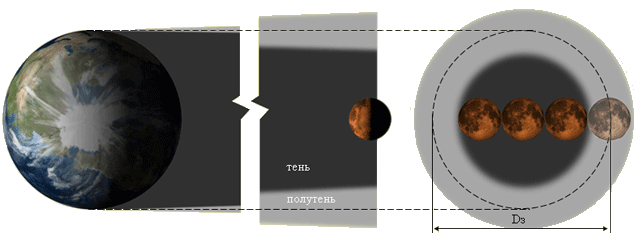
Из схемы видно, что диаметр Земли больше диаметра ее тени примерно на один поперечник Луны. Ну а зная реальный размер Земли, можно вычислить диаметр Луны и расстояние до нее.

Теперь мы можем легко определить и расстояние до нашего спутника. Правда, здесь мы отступим от методов древнегреческих астрономов, воспользовавшись неизвестными во времена Аристарха тригонометрическими выражениями. Отношение диаметра Луны к расстоянию до нее есть тангенс видимого углового размера Луны. Так как этот угол мал и равен примерно 1/2 °, мы можем считать, что тангенс угла равен величине угла, выраженной в радианах. Тогда расстояние до Луны

(Если бы мы хотели получить еще большую точность, то нам необходимо было бы точно определить угловой размер Луны - это нетрудно сделать, зная характеристики телескопа и фотоаппарата, и учесть, что наблюдатель находится не в центре Земли, но в этом примере некоторое ухудшение точности сознательно допущено для упрощения расчетов)

Аристарх, выполняя такие же расчеты, считал, что тень Земли ровно вдвое больше Луны, поэтому его оценка оказалась не очень точной. Он завысил размеры Луны и, соответственно, расстояние до нее примерно на 25%, однако этот результат был великим достижением уже хотя бы потому, что был получен научными методами - в результате наблюдений и расчетов. Кстати, только определение видимого размера Луны (а мы использовали эту величину для расчета расстояния до нее) в древности представляло собой непростую задачу...

Конечно, такой способ годится только для приближенной оценки, ведь орбиты Луны и Земли эллиптические и расстояния между небесными телами заметно изменяются, однако не забывайте, что нам удалось определить строение системы Земля-Луна практически без тригонометрических расчетов и не пользуясь никакими астрономическими приборами, кроме гномона!